What is Reinforcement Learning?

Short answer

Reinforcement learning (RL) is an optimization framework.

Long answer

A problem can be considered a reinforcement learning problem if it can be framed in the following way: Given an enviroment in which an agent can take actions, receiving a reward for each action, find a policy that maximizes the expected cumulative reward that the agent will obtain by acting in the environment.

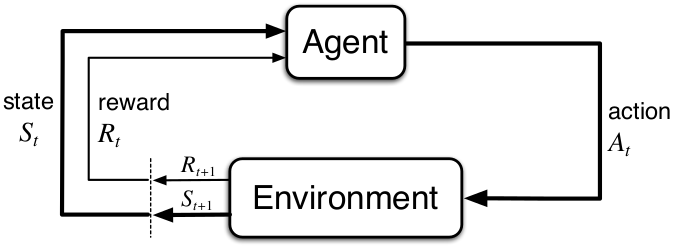
Markov Decision Processes

The most famous mathematical structure used to represent reinforcement learning environments are Markov Decision Processes (MDP). (Bellman1957) introduced the concept of a Markov Decision Process as an extension of the famous mathematical construct of Markov chains. Markov Decision Processes are a standard model for sequential decision making and control problems. An MDP is fully defined by the 5-tuple $(\mathcal{S}, \mathcal{A}, \mathcal{P(\cdot \vert \cdot, \cdot)}, \mathcal{R(\cdot, \cdot)}, \gamma)$. Whereby:

• $\mathcal{S}$ is the set of states $s \in \mathcal{S}$ of the underlying Markov chain, where $s_t \in \mathcal{S}$ represents the state of the environment at time $t$.

• $\mathcal{A}$ is the set of actions $a \in \mathcal{A}$ which are the transition labels between states of the underlying Markov chain. $A_t \subset \mathcal{A}$ is the subset of available actions in state $s_t$ at time $t$. If an state $s_t$ has no available actions, it is said to be a \textit{terminal} state.

• $\mathcal{P}(s_{t+1} \vert s_t, a_t) \in [0, 1]$, where $s_t, s_{t+1} \in \mathcal{S}$, $a_t \in \mathcal{A}$. $\mathcal{P}$ is the transition probability function (The function $\mathcal{P}$ is also known in the literature as the transition probability kernel, or the transition kernel. The word kernel is a heavily overloaded mathematical term that refers to a function that maps a series of inputs to value in $\mathbb{R}$). It defines the probability of transitioning to state $s_{t+1}$ from state $s_t$ after performig action $a_t$. Thus, $\mathcal{P}: \mathcal{S} \times \mathcal{A} \to [0,1]$. Given a state $s_t$ and an action $a_t$ at time $t$, we can find the next state $s_{t+1}$ by sampling from the distribution $s_{t+1} \sim P(s_t, a_t)$.

• $\mathcal{R}(s_t, a_t, s_{t+1}) \in \mathbb{R}$, where $s_t, s_{t+1} \in \mathcal{S}$, $a_t \in \mathcal{A}$. $\mathcal{R}$ is the reward function, which returns the immediate reward of performing action $a_t$ in state $s_t$ and ending in state $s_{t+1}$. The real-valued reward (The reward $r_t$ can be equivalently written as $r(s_t, a_t)$) $r_t$ is typically in the range $[-1,-1]$. $\mathcal{R}: \mathcal{S} \times \mathcal{A} \times \mathcal{S} \to \mathbb{R}$. If the environment is deterministic, the reward function can be rewritten as $\mathcal{R}(s_t, a_t)$ because the state transition defined by $\mathcal{P}(s_t, a_t)$ is deterministic.

• $\gamma \in [0,1]$ is the discount factor, which represent the rate of importance between immediate and future rewards. If $\gamma = 0$ the agent cares only about the immediate reward, if $\gamma = 1$ all rewards $r_t$ are taken into account. $\gamma$ is often used as a variance reduction method, and aids proofs in infinitely running environments (Sutton 1999).

The environment is sometimes represented by the Greek letter $\xi$. The tuple of elementes introduced above are the core components of any environment $\xi$. Finally, a lot of work in RL literature also presents a distribution over initial states $\rho_0$ of the MDP, So that the initial state can be sampled from it: $s_0 \sim \rho_0$.

An environment can be episodic if it presents terminal states, or if there are a fixed number of steps after which the environment will not accept any more actions. However environments can also run infinitely.

Acting inside of the environment, there is the agent, and through its actions the transitions between the MDP states are triggered, advancing the environment state and obtaining rewards. The agent’s behaviour is fully defined by its policy $\pi$. A policy $\pi(a_t \vert s_t) \in [0,1]$, where $s_t \in \mathcal{S}$, $a_t \in \mathcal{A}$ is a mapping from states to a distribution over actions. Given a state $s_t$ it is possible to sample an action $a_t$ from the policy distribution $a_t \sim \pi(s_t)$. Thus, $\pi: \mathcal{S} \times \mathcal{A} \to [0,1]$.

The reinforcement learning loop presented in image above can be represented in algorithmic form as follows:

1. Sample initial state from the initial state distribution $s_0 \sim \rho_0$
2. $t \leftarrow 0$.
   Repeat until $Termination$
3. $\;\;\;$ Sample action $a_t \sim \pi(s_t)$
4. $\;\;\;$ Sample successor state from the transition probability function $s_{t+1} \sim P(s_t, a_t)$
5. $\;\;\;$ Sample reward from reward function $r_t \sim R(s_t, a_t, s_{t+1})$
6. $\;\;\;$ $t \leftarrow t + 1$

For an episode of length $T$, The objective for the agent is to find an optimal policy $\pi^*$, which maximizes the cumulative sum of (possibly discounted) rewards.

Time for References!